| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 to 7 (Before Exercise 7.1) | Exercise 7.1 | Example 8 to 15 (Before Exercise 7.2) |
| Exercise 7.2 | ||
Chapter 7 Comparing Quantities
Welcome to the comprehensive solutions guide for Chapter 7, "Comparing Quantities," from the latest Class 7 NCERT mathematics textbook prescribed for the academic session 2024-25. This chapter is exceptionally practical, equipping students with essential mathematical tools needed to compare different quantities effectively and understand various financial concepts encountered in daily life. It bridges the gap between abstract numbers and real-world applications, focusing on ratios, proportions, percentages, and their crucial uses in calculating profit, loss, and simple interest. These solutions are designed to provide detailed, step-by-step methods for all exercises, fostering both conceptual clarity and computational accuracy.
The exploration begins with Ratios and Proportions. Ratios are used to compare two quantities of the same kind by division. The solutions demonstrate how to find the ratio between two quantities, emphasizing the critical step of ensuring they are in the same units before forming the ratio (often expressed in its simplest form, like a fraction $\frac{a}{b}$). Finding equivalent ratios (similar to equivalent fractions) and comparing different ratios are key skills covered. Building upon this, the concept of Proportion is explained, which states the equality of two ratios (i.e., if $a:b$ is proportional to $c:d$, then $\frac{a}{b} = \frac{c}{d}$). Solved examples illustrate how to check for proportionality and solve problems involving proportional relationships.
A significant portion of the chapter, and thus these solutions, is devoted to Percentages. Representing a fraction out of one hundred ($x\% = \frac{x}{100}$), percentages provide a standardized way to compare parts of a whole. The solutions meticulously cover:
- Converting between percentages, fractions, and decimals (e.g., converting $\frac{3}{4}$ to $75\%$, or $0.25$ to $25\%$, and vice versa).
- Calculating a specific percentage of a given quantity (e.g., finding $20\%$ of 150).
- Expressing one quantity as a percentage of another (e.g., determining what percentage 15 is of 60).
- Calculating percentage increase or percentage decrease, a common application in comparing values over time or analyzing changes.
Crucially, the solutions provide robust guidance on applying percentages to fundamental concepts in commercial mathematics, specifically Profit and Loss. Clear explanations are provided for key terms: Cost Price (CP - the price at which an item is bought), Selling Price (SP - the price at which an item is sold), Profit (when SP > CP), and Loss (when CP > SP). The solutions demonstrate step-by-step calculations for:
- Profit Amount: $\text{Profit} = \text{SP} - \text{CP}$
- Loss Amount: $\text{Loss} = \text{CP} - \text{SP}$
- Profit Percentage: $\text{Profit} \% = \left( \frac{\text{Profit}}{\text{CP}} \right) \times 100 \%$
- Loss Percentage: $\text{Loss} \% = \left( \frac{\text{Loss}}{\text{CP}} \right) \times 100 \%$
Furthermore, the chapter introduces Simple Interest (SI), a basic form of calculating interest earned or paid on a sum of money. The solutions explain the core terms: Principal (P - the initial amount of money borrowed or invested), Rate of Interest (R - the percentage at which interest is charged per period, usually per annum), and Time Period (T - the duration for which the money is borrowed or invested, typically in years). The solutions provide detailed application of the fundamental formula: $SI = \frac{P \times R \times T}{100}$ They also guide students in calculating the total Amount (A) to be repaid or received, which is the sum of the principal and the simple interest: $A = P + SI$.
Regarding the rationalized syllabus for 2024-25, Chapter 7, "Comparing Quantities," in the Class 7 NCERT textbook has maintained its focus on the essential concepts of Ratios, Percentages, Profit & Loss, and Simple Interest. The rationalization primarily involved streamlining the complexity and number of exercises, removing some intricate comparison methods or overly complex word problems, to ensure a solid grasp of core applications without excessive difficulty. By diligently working through these comprehensive solutions, students can master techniques for comparing quantities, become highly proficient in percentage calculations and their diverse real-world applications, understand fundamental financial concepts, and accurately calculate simple interest, thereby building essential numeracy skills.
Example 1 to 7 (Before Exercise 7.1)
Example 1. Write $\frac{1}{3}$ as per cent.
Answer:
Given:
The fraction $\frac{1}{3}$.
To Convert:
Write $\frac{1}{3}$ as a percentage.
Solution:
To convert a fraction into a percentage, we multiply the fraction by 100%.
So, we need to calculate:
$\frac{1}{3} \times 100\%$
Multiply the fraction by 100:
$\frac{1}{3} \times 100 = \frac{1 \times 100}{3} = \frac{100}{3}$
Now, we can express the fraction $\frac{100}{3}$ as a mixed number or a decimal.
As a mixed number:
When 100 is divided by 3, the quotient is 33 and the remainder is 1.
So, $\frac{100}{3} = 33 \frac{1}{3}$.
As a decimal:
$\frac{100}{3} \approx 33.333...$
Therefore, the percentage is $33 \frac{1}{3}\%$ or approximately $33.33\%$.
Answer:
$\frac{1}{3}$ as per cent is $33 \frac{1}{3}\%$ or approximately $33.33\%$.
Example 2. Out of 25 children in a class, 15 are girls. What is the percentage of girls?
Answer:
Given:
Total number of children in a class = 25.
Number of girls = 15.
To Find:
The percentage of girls in the class.
Solution:
To find the percentage of girls, we need to express the number of girls as a fraction of the total number of children and then convert that fraction into a percentage.
The fraction of girls in the class is the number of girls divided by the total number of children:
Fraction of girls = $\frac{\text{Number of girls}}{\text{Total number of children}} = \frac{15}{25}$
To convert this fraction to a percentage, we multiply by 100%:
Percentage of girls = $\left(\frac{15}{25}\right) \times 100\%$
Simplify the fraction $\frac{15}{25}$ by dividing the numerator and denominator by their greatest common divisor, which is 5:
$\frac{15}{25} = \frac{\cancel{15}^{3}}{\cancel{25}_{5}} = \frac{3}{5}$
Now, substitute the simplified fraction back into the percentage calculation:
Percentage of girls = $\frac{3}{5} \times 100\%$
Multiply the fraction by 100:
Percentage of girls = $\frac{3 \times 100}{5}\%$
Percentage of girls = $\frac{300}{5}\%$
Perform the division:
$\frac{300}{5} = 60$
So, the percentage of girls is 60%.
Answer:
The percentage of girls is 60%.
Example 3. Convert $\frac{5}{4}$ to per cent.
Answer:
Given:
The fraction $\frac{5}{4}$.
To Convert:
Write $\frac{5}{4}$ as a percentage.
Solution:
To convert a fraction into a percentage, we multiply the fraction by 100%.
So, we need to calculate:
$\frac{5}{4} \times 100\%$
Multiply the fraction by 100:
$\frac{5}{4} \times 100 = \frac{5 \times 100}{4} = \frac{500}{4}$
Perform the division:
$\frac{500}{4} = 125$
Therefore, the percentage is 125%.
This means that $\frac{5}{4}$ is equal to 125%.
Answer:
$\frac{5}{4}$ converted to per cent is 125%.
Example 4. Convert the given decimals to per cents:
(a) 0.75
(b) 0.09
(c) 0.2
Answer:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the '%' symbol.
(a) Convert 0.75 to per cent.
Given: The decimal 0.75.
To Convert: Write 0.75 as a percentage.
Solution:
$0.75 \times 100\% = 75\%$
Answer: 0.75 as per cent is 75%.
(b) Convert 0.09 to per cent.
Given: The decimal 0.09.
To Convert: Write 0.09 as a percentage.
Solution:
$0.09 \times 100\% = 9\%$
Answer: 0.09 as per cent is 9%.
(c) Convert 0.2 to per cent.
Given: The decimal 0.2.
To Convert: Write 0.2 as a percentage.
Solution:
$0.2 \times 100\% = 20\%$
Answer: 0.2 as per cent is 20%.
Example 5. What per cent of the adjoining figure is shaded?

Answer:
Solution:
Given:
The figure shows a rectangle divided into equal parts.
Total number of equal parts in the figure = 3.
Number of shaded parts = 1 + $\frac{1}{2}$.
Number of shaded parts = $\frac{2}{2} + \frac{1}{2} = \frac{3}{2}$.
To Find:
The percentage of the figure that is shaded.
Solution:
To find the percentage of the shaded area, we first need to find the fraction of the shaded area.
Fraction of shaded area = $\frac{\text{Number of shaded parts}}{\text{Total number of parts}}$
... (i)
Substitute the given values into equation (i):
Fraction of shaded area = $\frac{\frac{3}{2}}{3}$
Now, simplify the fraction:
$\frac{\frac{3}{2}}{3} = \frac{3}{2} \div 3 = \frac{3}{2} \times \frac{1}{3}$
Multiply the numerators and the denominators:
$\frac{3 \times 1}{2 \times 3} = \frac{3}{6}$
Simplify the fraction $\frac{3}{6}$ by dividing both numerator and denominator by their greatest common divisor, which is 3:
$\frac{3 \div 3}{6 \div 3} = \frac{1}{2}$
So, the fraction of the shaded area is $\frac{1}{2}$.
Now, to convert this fraction into a percentage, we multiply it by $100\%$.
Percentage of shaded area = Fraction of shaded area $\times 100\%$
... (ii)
Substitute the simplified fraction into equation (ii):
Percentage of shaded area = $\frac{1}{2} \times 100\%$
Percentage of shaded area = $\frac{100}{2} \%$
Divide 100 by 2:
Percentage of shaded area = $50 \%$
Answer:
The percentage of the adjoining figure that is shaded is $50 \%$.
Example 6. A survey of 40 children showed that 25% liked playing football. How many children liked playing football?
Answer:
Given:
Total number of children surveyed = 40.
Percentage of children who liked playing football = 25%.
To Find:
The number of children who liked playing football.
Solution:
To find the number of children who liked playing football, we need to calculate 25% of the total number of children.
Percentage means 'out of one hundred'. So, 25% can be written as a fraction $\frac{25}{100}$ or as a decimal 0.25.
To find a percentage of a number, we multiply the number by the percentage (as a fraction or decimal).
Number of children who liked football = 25% of 40
Using the fraction form:
Number of children = $\frac{25}{100} \times 40$
We can simplify the fraction $\frac{25}{100}$:
$\frac{25}{100} = \frac{\cancel{25}^{1}}{\cancel{100}_{4}} = \frac{1}{4}$
Now, calculate the number of children:
Number of children = $\frac{1}{4} \times 40$
Number of children = $\frac{40}{4}$
Number of children = 10
Using the decimal form:
Number of children = $0.25 \times 40$
$0.25 \times 40 = 10.00$
Number of children = 10
Both methods give the same result.
Answer:
The number of children who liked playing football is 10.
Example 7. Rahul bought a sweater and saved ₹ 200 when a discount of 25% was given. What was the price of the sweater before the discount?
Answer:
Given:
Amount of discount = $\textsf{₹}$ 200.
Percentage of discount = 25%.
To Find:
The original price of the sweater before the discount.
Solution:
Let the original price of the sweater be $P$.
The discount is given as a percentage of the original price.
We are given that the discount amount is $\textsf{₹}$ 200, and this discount is 25% of the original price.
So, we can write the relationship:
25% of Original Price = Discount Amount
25% of $P$ = $\textsf{₹}$ 200
We can express 25% as a fraction or a decimal.
As a fraction, 25% = $\frac{25}{100}$.
The equation becomes:
$\frac{25}{100} \times P = 200$
Simplify the fraction $\frac{25}{100}$:
$\frac{\cancel{25}^{1}}{\cancel{100}_{4}} = \frac{1}{4}$
Substitute the simplified fraction back into the equation:
$\frac{1}{4} \times P = 200$
To solve for $P$, multiply both sides of the equation by 4:
$P = 200 \times 4$
$P = 800$
Using the decimal form, 25% = 0.25.
The equation becomes:
$0.25 \times P = 200$
To solve for $P$, divide both sides of the equation by 0.25:
$P = \frac{200}{0.25}$
$P = \frac{200}{\frac{1}{4}} = 200 \times 4 = 800$
So, the original price of the sweater was $\textsf{₹}$ 800.
We can verify this: 25% of $\textsf{₹}$ 800 = $\frac{25}{100} \times 800 = \frac{1}{4} \times 800 = \textsf{₹}$ 200. This matches the given discount amount.
Answer:
The price of the sweater before the discount was $\textsf{₹}$ 800.
Exercise 7.1
Question 1. Convert the given fractional numbers to per cents.
(a) $\frac{1}{8}$
(b) $\frac{5}{4}$
(c) $\frac{3}{40}$
(d) $\frac{2}{7}$
Answer:
To convert a fractional number to a percentage, we multiply the fraction by 100%.
(a) $\frac{1}{8}$
Given: The fraction $\frac{1}{8}$.
To Convert: Write $\frac{1}{8}$ as a percentage.
Solution:
Percentage = $\frac{1}{8} \times 100\%$
Percentage = $\frac{100}{8}\%$
Simplify the fraction:
$\frac{\cancel{100}^{25}}{\cancel{8}_{2}} = \frac{25}{2}$
Percentage = $\frac{25}{2}\%$
Percentage = $12.5\%$
(b) $\frac{5}{4}$
Given: The fraction $\frac{5}{4}$.
To Convert: Write $\frac{5}{4}$ as a percentage.
Solution:
Percentage = $\frac{5}{4} \times 100\%$
Percentage = $\frac{5 \times 100}{4}\%$
Percentage = $\frac{500}{4}\%$
Perform the division:
Percentage = $125\%$
(c) $\frac{3}{40}$
Given: The fraction $\frac{3}{40}$.
To Convert: Write $\frac{3}{40}$ as a percentage.
Solution:
Percentage = $\frac{3}{40} \times 100\%$
Percentage = $\frac{3 \times 100}{40}\%$
Percentage = $\frac{300}{40}\%$
Simplify the fraction:
$\frac{\cancel{300}^{15}}{\cancel{40}_{2}} = \frac{15}{2}$
Percentage = $\frac{15}{2}\%$
Percentage = $7.5\%$
(d) $\frac{2}{7}$
Given: The fraction $\frac{2}{7}$.
To Convert: Write $\frac{2}{7}$ as a percentage.
Solution:
Percentage = $\frac{2}{7} \times 100\%$
Percentage = $\frac{2 \times 100}{7}\%$
Percentage = $\frac{200}{7}\%$
This can be left as a fraction or converted to a mixed number or decimal.
As a mixed number:
$\frac{200}{7} = 28 \frac{4}{7}$
Percentage = $28 \frac{4}{7}\%$
As a decimal (approximate):
$\frac{200}{7} \approx 28.57$
Percentage $\approx$ $28.57\%$
Question 2. Convert the given decimal fractions to per cents.
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Answer:
To convert a decimal fraction to a percentage, we multiply the decimal by 100 and add the '%' symbol. This is because 'per cent' means 'out of one hundred'. Multiplying by 100 effectively tells us how many hundredths the decimal represents.
(a) 0.65
Given: The decimal is 0.65.
To Convert: Write 0.65 as a percentage.
Solution:
We multiply the decimal 0.65 by 100 to convert it into a percentage.
Percentage = $0.65 \times 100$
To multiply a decimal by 100, we shift the decimal point two places to the right.
$0.65 \times 100 = 65$
Now, add the percentage symbol ($\%$).
Percentage = $65\%$
(b) 2.1
Given: The decimal is 2.1.
To Convert: Write 2.1 as a percentage.
Solution:
We multiply the decimal 2.1 by 100 to convert it into a percentage.
Percentage = $2.1 \times 100$
Shift the decimal point two places to the right. We need to add a zero after 1.
$2.1 \times 100 = 210$
Now, add the percentage symbol ($\%$).
Percentage = $210\%$
(c) 0.02
Given: The decimal is 0.02.
To Convert: Write 0.02 as a percentage.
Solution:
We multiply the decimal 0.02 by 100 to convert it into a percentage.
Percentage = $0.02 \times 100$
Shift the decimal point two places to the right.
$0.02 \times 100 = 2$
Now, add the percentage symbol ($\%$).
Percentage = $2\%$
(d) 12.35
Given: The decimal is 12.35.
To Convert: Write 12.35 as a percentage.
Solution:
We multiply the decimal 12.35 by 100 to convert it into a percentage.
Percentage = $12.35 \times 100$
Shift the decimal point two places to the right.
$12.35 \times 100 = 1235$
Now, add the percentage symbol ($\%$).
Percentage = $1235\%$
Question 3. Estimate what part of the figures is coloured and hence find the per cent which is coloured.
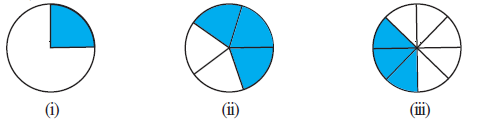
Answer:
To find the percentage of the coloured part, we first determine the fraction of the figure that is coloured and then convert that fraction into a percentage by multiplying by 100%.
Figure 1:
Observe the circle. It is divided into 4 equal parts.
The number of coloured parts is 1.
The fraction of the coloured part is $\frac{\text{Number of coloured parts}}{\text{Total number of parts}} = \frac{1}{4}$.
To find the percentage, multiply the fraction by 100%:
Percentage coloured = $\frac{1}{4} \times 100\%$
Percentage coloured = $\frac{100}{4}\%$
Percentage coloured = $25\%$
Figure 2:
Observe the circle. It is divided into 5 equal parts.
The number of coloured parts is 3.
The fraction of the coloured part is $\frac{\text{Number of coloured parts}}{\text{Total number of parts}} = \frac{3}{5}$.
To find the percentage, multiply the fraction by 100%:
Percentage coloured = $\frac{3}{5} \times 100\%$
Percentage coloured = $\frac{3 \times 100}{5}\%$
Percentage coloured = $\frac{300}{5}\%$
Percentage coloured = $60\%$
Figure 3:
Observe the circle. It is divided into 8 equal parts.
The number of coloured parts is 3.
The fraction of the coloured part is $\frac{\text{Number of coloured parts}}{\text{Total number of parts}} = \frac{3}{8}$.
To find the percentage, multiply the fraction by 100%:
Percentage coloured = $\frac{3}{8} \times 100\%$
Percentage coloured = $\frac{300}{8}\%$
Simplify the fraction:
Percentage coloured = $\frac{\cancel{300}^{75}}{\cancel{8}_{2}}\%$
Percentage coloured = $\frac{75}{2}\%$
Percentage coloured = $37.5\%$
Question 4. Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of ₹ 2500
(d) 75% of 1 kg
Answer:
To find a percentage of a quantity, we convert the percentage to a fraction or a decimal and then multiply it by the quantity.
(a) 15% of 250
Given: Find 15% of the quantity 250.
Solution:
Convert 15% to a fraction: $15\% = \frac{15}{100}$
Now, calculate 15% of 250:
$15\% \text{ of } 250 = \frac{15}{100} \times 250$
$= \frac{15 \times \cancel{250}^{5}}{\cancel{100}_{2}} = \frac{15 \times 5}{2} = \frac{75}{2}$
$= 37.5$
Answer: 15% of 250 is 37.5.
(b) 1% of 1 hour
Given: Find 1% of the quantity 1 hour.
Solution:
Convert 1% to a fraction: $1\% = \frac{1}{100}$
Also, 1 hour = 60 minutes.
Now, calculate 1% of 1 hour (in minutes):
$1\% \text{ of } 60 \text{ minutes} = \frac{1}{100} \times 60 \text{ minutes}$
$= \frac{60}{100} \text{ minutes}$
Simplify the fraction:
$= \frac{\cancel{60}^{3}}{\cancel{100}_{5}} = \frac{3}{5}$ minutes
We can also convert this to seconds:
$\frac{3}{5} \text{ minutes} = \frac{3}{5} \times 60 \text{ seconds}$
$= 3 \times \cancel{\frac{60}{5}}^{12} = 3 \times 12 = 36$ seconds
Answer: 1% of 1 hour is $\frac{3}{5}$ minutes or 36 seconds.
(c) 20% of $\textsf{₹}$ 2500
Given: Find 20% of the quantity $\textsf{₹}$ 2500.
Solution:
Convert 20% to a fraction: $20\% = \frac{20}{100}$
Now, calculate 20% of $\textsf{₹}$ 2500:
$20\% \text{ of } \textsf{₹}\ 2500 = \frac{20}{100} \times 2500$
$= \frac{\cancel{20}^{1}}{\cancel{100}_{5}} \times 2500 = \frac{1}{5} \times 2500$
$= \frac{2500}{5} = 500$
Answer: 20% of $\textsf{₹}$ 2500 is $\textsf{₹}$ 500.
(d) 75% of 1 kg
Given: Find 75% of the quantity 1 kg.
Solution:
Convert 75% to a fraction: $75\% = \frac{75}{100}$
Also, 1 kg = 1000 grams.
Now, calculate 75% of 1 kg (in grams):
$75\% \text{ of } 1000 \text{ g} = \frac{75}{100} \times 1000 \text{ g}$
$= \frac{\cancel{75}^{3}}{\cancel{100}_{4}} \times 1000 \text{ g} = \frac{3}{4} \times 1000 \text{ g}$
$= \frac{3 \times 1000}{4} \text{ g} = \frac{3000}{4} \text{ g} = 750 \text{ g}$
Alternatively, we can leave the answer in kg:
$75\% \text{ of } 1 \text{ kg} = \frac{75}{100} \times 1 \text{ kg} = \frac{3}{4} \text{ kg}$
Answer: 75% of 1 kg is $\frac{3}{4}$ kg or 750 g.
Question 5. Find the whole quantity if
(a) 5% of it is 600.
(b) 12% of it is ₹ 1080.
(c) 40% of it is 500 km.
(d) 70% of it is 14 minutes.
(e) 8% of it is 40 litres.
Answer:
In each case, let the whole quantity be represented by 'x'. We are given a percentage of this quantity is equal to a specific value. We can write an equation and solve for x.
(a) 5% of it is 600.
Given: 5% of the whole quantity is 600.
To Find: The whole quantity.
Solution:
Let the whole quantity be x.
5% of x = 600
Convert 5% to a fraction: $5\% = \frac{5}{100}$
$\frac{5}{100} \times x = 600$
Simplify the fraction: $\frac{\cancel{5}^{1}}{\cancel{100}_{20}} = \frac{1}{20}$
$\frac{1}{20} \times x = 600$
Multiply both sides by 20 to solve for x:
$x = 600 \times 20$
$x = 12000$
Answer: The whole quantity is 12000.
(b) 12% of it is ₹ 1080.
Given: 12% of the whole quantity is $\textsf{₹}$ 1080.
To Find: The whole quantity.
Solution:
Let the whole quantity be x.
12% of x = $\textsf{₹}$ 1080
Convert 12% to a fraction: $12\% = \frac{12}{100}$
$\frac{12}{100} \times x = 1080$
Multiply both sides by $\frac{100}{12}$ to solve for x:
$x = 1080 \times \frac{100}{12}$
$x = \cancel{\frac{1080}{12}}^{90} \times 100$
$x = 90 \times 100$
$x = 9000$
Answer: The whole quantity is $\textsf{₹}$ 9000.
(c) 40% of it is 500 km.
Given: 40% of the whole quantity is 500 km.
To Find: The whole quantity.
Solution:
Let the whole quantity be x.
40% of x = 500 km
Convert 40% to a fraction: $40\% = \frac{40}{100}$
$\frac{40}{100} \times x = 500$
Simplify the fraction: $\frac{\cancel{40}^{2}}{\cancel{100}_{5}} = \frac{2}{5}$
$\frac{2}{5} \times x = 500$
Multiply both sides by $\frac{5}{2}$ to solve for x:
$x = 500 \times \frac{5}{2}$
$x = \cancel{\frac{500}{2}}^{250} \times 5$
$x = 250 \times 5$
$x = 1250$
Answer: The whole quantity is 1250 km.
(d) 70% of it is 14 minutes.
Given: 70% of the whole quantity is 14 minutes.
To Find: The whole quantity.
Solution:
Let the whole quantity be x.
70% of x = 14 minutes
Convert 70% to a fraction: $70\% = \frac{70}{100}$
$\frac{70}{100} \times x = 14$
Simplify the fraction: $\frac{\cancel{70}^{7}}{\cancel{100}_{10}} = \frac{7}{10}$
$\frac{7}{10} \times x = 14$
Multiply both sides by $\frac{10}{7}$ to solve for x:
$x = 14 \times \frac{10}{7}$
$x = \cancel{\frac{14}{7}}^{2} \times 10$
$x = 2 \times 10$
$x = 20$
Answer: The whole quantity is 20 minutes.
(e) 8% of it is 40 litres.
Given: 8% of the whole quantity is 40 litres.
To Find: The whole quantity.
Solution:
Let the whole quantity be x.
8% of x = 40 litres
Convert 8% to a fraction: $8\% = \frac{8}{100}$
$\frac{8}{100} \times x = 40$
Simplify the fraction: $\frac{\cancel{8}^{2}}{\cancel{100}_{25}} = \frac{2}{25}$
$\frac{2}{25} \times x = 40$
Multiply both sides by $\frac{25}{2}$ to solve for x:
$x = 40 \times \frac{25}{2}$
$x = \cancel{\frac{40}{2}}^{20} \times 25$
$x = 20 \times 25$
$x = 500$
Answer: The whole quantity is 500 litres.
Question 6. Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Answer:
To convert a percentage to a decimal, we divide the percentage by 100.
To convert a percentage to a fraction, we write the percentage as a fraction with a denominator of 100 and then simplify it to its simplest form.
(a) 25%
Given: The percentage 25%.
To Convert: To a decimal fraction and a fraction in simplest form.
Solution:
Convert to decimal fraction:
25% = $\frac{25}{100} = 0.25$
Convert to fraction in simplest form:
25% = $\frac{25}{100}$
Divide the numerator and denominator by their greatest common divisor, 25:
$\frac{\cancel{25}^{1}}{\cancel{100}_{4}} = \frac{1}{4}$
Answer:
Decimal fraction: 0.25
Fraction in simplest form: $\frac{1}{4}$
(b) 150%
Given: The percentage 150%.
To Convert: To a decimal fraction and a fraction in simplest form.
Solution:
Convert to decimal fraction:
150% = $\frac{150}{100} = 1.50$ or $1.5$
Convert to fraction in simplest form:
150% = $\frac{150}{100}$
Divide the numerator and denominator by their greatest common divisor, 50:
$\frac{\cancel{150}^{3}}{\cancel{100}_{2}} = \frac{3}{2}$
Answer:
Decimal fraction: 1.5
Fraction in simplest form: $\frac{3}{2}$
(c) 20%
Given: The percentage 20%.
To Convert: To a decimal fraction and a fraction in simplest form.
Solution:
Convert to decimal fraction:
20% = $\frac{20}{100} = 0.20$ or $0.2$
Convert to fraction in simplest form:
20% = $\frac{20}{100}$
Divide the numerator and denominator by their greatest common divisor, 20:
$\frac{\cancel{20}^{1}}{\cancel{100}_{5}} = \frac{1}{5}$
Answer:
Decimal fraction: 0.2
Fraction in simplest form: $\frac{1}{5}$
(d) 5%
Given: The percentage 5%.
To Convert: To a decimal fraction and a fraction in simplest form.
Solution:
Convert to decimal fraction:
5% = $\frac{5}{100} = 0.05$
Convert to fraction in simplest form:
5% = $\frac{5}{100}$
Divide the numerator and denominator by their greatest common divisor, 5:
$\frac{\cancel{5}^{1}}{\cancel{100}_{20}} = \frac{1}{20}$
Answer:
Decimal fraction: 0.05
Fraction in simplest form: $\frac{1}{20}$
Question 7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?
Answer:
Given:
Percentage of females in the city = 30%.
Percentage of males in the city = 40%.
The remaining population are children.
To Find:
The percentage of children in the city.
Solution:
The total population of the city represents 100%.
The population is divided into three categories: females, males, and children.
The sum of the percentages of these categories must equal 100%.
Percentage of females + Percentage of males + Percentage of children = 100%
Substitute the given percentages for females and males:
30% + 40% + Percentage of children = 100%
Add the percentages of females and males:
70% + Percentage of children = 100%
To find the percentage of children, subtract 70% from 100%:
Percentage of children = 100% - 70%
Percentage of children = 30%
Answer:
The percentage of children is 30%.
Question 8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Answer:
Given:
Total number of voters in a constituency = 15,000.
Percentage of voters who voted = 60%.
To Find:
The percentage of voters who did not vote.
The number of voters who actually did not vote.
Solution:
The total percentage of voters in the constituency is 100%.
The voters can be divided into two groups: those who voted and those who did not vote.
So, Percentage of voters who voted + Percentage of voters who did not vote = 100%.
Substitute the given percentage of voters who voted:
60% + Percentage of voters who did not vote = 100%
To find the percentage of voters who did not vote, subtract 60% from 100%:
Percentage of voters who did not vote = 100% - 60%
Percentage of voters who did not vote = 40%
So, 40% of the voters did not vote.
Now, we can find the actual number of voters who did not vote.
The number of voters who did not vote is 40% of the total number of voters (15,000).
Convert 40% to a fraction: $40\% = \frac{40}{100}$
Number of voters who did not vote = 40% of 15,000
Number of voters who did not vote = $\frac{40}{100} \times 15000$
Number of voters who did not vote = $\frac{\cancel{40}^{2}}{\cancel{100}_{5}} \times 15000$
Number of voters who did not vote = $\frac{2}{5} \times 15000$
Number of voters who did not vote = $\frac{2 \times \cancel{15000}^{3000}}{\cancel{5}_{1}}$
Number of voters who did not vote = $2 \times 3000$
Number of voters who did not vote = 6000
So, 6000 voters did not vote.
Yes, we can find the number of voters who actually did not vote.
Answer:
The percentage of voters who did not vote is 40%.
The number of voters who actually did not vote is 6000.
Question 9. Meeta saves ₹4000 from her salary. If this is 10% of her salary. What is her salary?
Answer:
Given:
Amount saved by Meeta = $\textsf{₹}$ 4000.
The amount saved is 10% of her salary.
To Find:
What is Meeta's total salary?
Solution:
Let Meeta's total salary be represented by S.
We are given that $\textsf{₹}$ 4000 is 10% of her salary.
This can be written as an equation:
10% of S = $\textsf{₹}$ 4000
To solve for S, we first convert the percentage to a fraction or a decimal.
Using the fraction form:
$10\% = \frac{10}{100}$
So the equation is:
$\frac{10}{100} \times \text{S} = 4000$
Simplify the fraction $\frac{10}{100}$:
$\frac{10}{100} = \frac{1}{10}$
The equation becomes:
$\frac{1}{10} \times \text{S} = 4000$
To find S, multiply both sides of the equation by 10:
$\text{S} = 4000 \times 10$
$\text{S} = 40000$
Using the decimal form:
$10\% = 0.10$
So the equation is:
$0.10 \times \text{S} = 4000$
To find S, divide both sides of the equation by 0.10:
$\text{S} = \frac{4000}{0.10}$
$\text{S} = 40000$
Both methods give the same result.
Meeta's total salary is $\textsf{₹}$ 40000.
Answer:
Meeta's salary is $\textsf{₹}$ 40000.
Question 10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Answer:
Given:
Total number of matches played by the team = 20.
Percentage of matches won by the team = 25%.
To Find:
The number of matches the team won.
Solution:
To find the number of matches won, we need to calculate 25% of the total number of matches played.
Percentage means 'out of one hundred'. So, 25% can be written as a fraction $\frac{25}{100}$ or as a decimal 0.25.
Number of matches won = 25% of Total matches played
Number of matches won = 25% of 20
Using the fraction form:
Number of matches won = $\frac{25}{100} \times 20$
Simplify the fraction $\frac{25}{100}$:
$\frac{25}{100} = \frac{\cancel{25}^{1}}{\cancel{100}_{4}} = \frac{1}{4}$
Now, calculate the number of matches won:
Number of matches won = $\frac{1}{4} \times 20$
Number of matches won = $\frac{20}{4}$
Number of matches won = 5
Using the decimal form:
Number of matches won = $0.25 \times 20$
$0.25 \times 20 = 5.00$
Number of matches won = 5
Both methods give the same result.
Answer:
The team won 5 matches.
Example 8 to 15 (Before Exercise 7.2)
Example 8. Reena’s mother said, to make idlis, you must take two parts rice and one part urad dal. What percentage of such a mixture would be rice and what percentage would be urad dal?
Answer:
Given:
Ratio of rice to urad dal for idlis = 2 parts rice : 1 part urad dal.
To Find:
Percentage of rice in the mixture.
Percentage of urad dal in the mixture.
Solution:
To find the percentage of each ingredient, we first need to find the total number of parts in the mixture.
Total parts = Parts of rice + Parts of urad dal
Total parts = 2 + 1 = 3 parts
Now, we find the fraction of each ingredient in the mixture.
Fraction of rice = $\frac{\text{Parts of rice}}{\text{Total parts}} = \frac{2}{3}$
Fraction of urad dal = $\frac{\text{Parts of urad dal}}{\text{Total parts}} = \frac{1}{3}$
To convert a fraction to a percentage, we multiply the fraction by 100%.
Percentage of rice = Fraction of rice $\times$ 100%
Percentage of rice = $\frac{2}{3} \times 100\%$
Percentage of rice = $\frac{200}{3}\%$
Percentage of rice = $66 \frac{2}{3}\%$ (or approximately $66.67\%$)
Percentage of urad dal = Fraction of urad dal $\times$ 100%
Percentage of urad dal = $\frac{1}{3} \times 100\%$
Percentage of urad dal = $\frac{100}{3}\%$
Percentage of urad dal = $33 \frac{1}{3}\%$ (or approximately $33.33\%$)
Check: $66 \frac{2}{3}\% + 33 \frac{1}{3}\% = (66+33) + (\frac{2}{3}+\frac{1}{3})\% = 99 + \frac{3}{3}\% = 99 + 1\% = 100\%$. This is correct.
Answer:
The percentage of rice in the mixture is $66 \frac{2}{3}\%$.
The percentage of urad dal in the mixture is $33 \frac{1}{3}\%$.
Example 9. If ₹ 250 is to be divided amongst Ravi, Raju and Roy, so that Ravi gets two parts, Raju three parts and Roy five parts. How much money will each get? What will it be in percentages?
Answer:
Given:
Total amount to be divided = $\textsf{₹}$ 250.
The amount is divided among Ravi, Raju, and Roy.
Share distribution in parts:
Ravi gets 2 parts.
Raju gets 3 parts.
Roy gets 5 parts.
To Find:
How much money each person will get.
The percentage share for each person.
Solution:
First, find the total number of parts into which the amount is divided.
Total number of parts = Parts of Ravi + Parts of Raju + Parts of Roy
Total parts = $2 + 3 + 5 = 10$ parts.
The total amount $\textsf{₹}$ 250 is divided into 10 equal parts.
The value of one part is the total amount divided by the total number of parts.
Value of one part = $\frac{\text{Total Amount}}{\text{Total parts}}$
Value of one part = $\frac{\textsf{₹}\ 250}{10} = \textsf{₹}\ 25$ per part.
Now, calculate the amount of money each person gets by multiplying the value of one part by their respective number of parts.
Amount Ravi gets = Parts of Ravi $\times$ Value of one part
Amount Ravi gets = $2 \times \textsf{₹}\ 25 = \textsf{₹}\ 50$
Amount Raju gets = Parts of Raju $\times$ Value of one part
Amount Raju gets = $3 \times \textsf{₹}\ 25 = \textsf{₹}\ 75$
Amount Roy gets = Parts of Roy $\times$ Value of one part
Amount Roy gets = $5 \times \textsf{₹}\ 25 = \textsf{₹}\ 125$
Let's verify the sum of the amounts: $\textsf{₹}\ 50 + \textsf{₹}\ 75 + \textsf{₹}\ 125 = \textsf{₹}\ 250$, which is the total amount.
Next, find the percentage share for each person.
The percentage share is the amount each person gets as a fraction of the total amount, multiplied by 100%.
Alternatively, we can use the number of parts directly as a fraction of the total parts.
Percentage share = $\frac{\text{Number of parts for the person}}{\text{Total number of parts}} \times 100\%$
Percentage share of Ravi = $\frac{2}{10} \times 100\%$
Percentage share of Ravi = $\frac{1}{5} \times 100\% = \frac{100}{5}\% = 20\%$
Percentage share of Raju = $\frac{3}{10} \times 100\%$
Percentage share of Raju = $\frac{3 \times 100}{10}\% = \frac{300}{10}\% = 30\%$
Percentage share of Roy = $\frac{5}{10} \times 100\%$
Percentage share of Roy = $\frac{1}{2} \times 100\% = \frac{100}{2}\% = 50\%$
Let's verify the sum of percentages: $20\% + 30\% + 50\% = 100\%$. This is correct.
Answer:
The amount of money each will get:
Ravi: $\textsf{₹}\ 50$
Raju: $\textsf{₹}\ 75$
Roy: $\textsf{₹}\ 125$
The percentage share for each:
Ravi: 20%
Raju: 30%
Roy: 50%
Example 10. A school team won 6 games this year against 4 games won last year. What is the per cent increase?
Answer:
Given:
Number of games won last year = 4.
Number of games won this year = 6.
To Find:
The per cent increase in the number of games won.
Solution:
First, we find the increase in the number of games won from last year to this year.
Increase in games won = Number of games won this year - Number of games won last year
Increase in games won = $6 - 4 = 2$ games.
To find the percentage increase, we compare the increase to the original number of games won (last year's number) and multiply by 100%.
Percentage Increase = $\frac{\text{Amount of Increase}}{\text{Original Amount}} \times 100\%$
Percentage Increase = $\frac{\text{Increase in games won}}{\text{Number of games won last year}} \times 100\%$
Substitute the values:
Percentage Increase = $\frac{2}{4} \times 100\%$
Simplify the fraction $\frac{2}{4}$:
Percentage Increase = $\frac{1}{2} \times 100\%$
Calculate the percentage:
Percentage Increase = $50\%$
Answer:
The per cent increase in the number of games won is 50%.
Example 11. The number of illiterate persons in a country decreased from 150 lakhs to 100 lakhs in 10 years. What is the percentage of decrease?
Answer:
Given:
Initial number of illiterate persons = 150 lakhs.
Final number of illiterate persons (after 10 years) = 100 lakhs.
To Find:
The percentage of decrease in the number of illiterate persons.
Solution:
First, calculate the actual decrease in the number of illiterate persons.
Decrease in number = Initial number - Final number
Decrease in number = 150 lakhs - 100 lakhs
Decrease in number = 50 lakhs
Now, calculate the percentage decrease. The percentage decrease is calculated with respect to the original amount (the initial number of illiterate persons).
Percentage Decrease = $\frac{\text{Amount of Decrease}}{\text{Original Amount}} \times 100\%$
Percentage Decrease = $\frac{50 \text{ lakhs}}{150 \text{ lakhs}} \times 100\%$
Simplify the fraction $\frac{50}{150}$:
$\frac{50}{150} = \frac{\cancel{50}^{1}}{\cancel{150}_{3}} = \frac{1}{3}$
Substitute the simplified fraction back into the percentage calculation:
Percentage Decrease = $\frac{1}{3} \times 100\%$
Percentage Decrease = $\frac{100}{3}\%$
This can be expressed as a mixed number or a decimal.
As a mixed number:
$\frac{100}{3}\% = 33 \frac{1}{3}\%$
As a decimal (approximate):
$\frac{100}{3}\% \approx 33.33\%$
Answer:
The percentage of decrease in the number of illiterate persons is $33 \frac{1}{3}\%$ (or approximately 33.33%).
Example 12. The cost of a flower vase is ₹ 120. If the shopkeeper sells it at a loss of 10%, find the price at which it is sold.
Answer:
Given:
Cost Price (CP) of the flower vase = $\textsf{₹}$ 120.
Loss Percentage = 10%.
To Find:
The Selling Price (SP) at which the flower vase is sold.
Solution:
The loss is calculated as a percentage of the Cost Price.
First, calculate the amount of loss in Rupees.
Loss Amount = Loss Percentage of Cost Price
Loss Amount = 10% of $\textsf{₹}$ 120
Convert 10% to a fraction: $10\% = \frac{10}{100}$
Loss Amount = $\frac{10}{100} \times \textsf{₹}\ 120$
Loss Amount = $\frac{1}{10} \times \textsf{₹}\ 120$
Loss Amount = $\textsf{₹}\ \frac{120}{10}$
Loss Amount = $\textsf{₹}\ 12$
The amount of loss is $\textsf{₹}$ 12.
The Selling Price is calculated by subtracting the Loss Amount from the Cost Price.
Selling Price (SP) = Cost Price (CP) - Loss Amount
SP = $\textsf{₹}\ 120 - \textsf{₹}\ 12$
SP = $\textsf{₹}\ 108$
Alternate Solution:
Selling at a loss of 10% means the Selling Price is (100% - 10%) of the Cost Price.
Selling Price Percentage = 100% - Loss Percentage
Selling Price Percentage = 100% - 10% = 90%
So, the Selling Price is 90% of the Cost Price.
Selling Price (SP) = 90% of CP
SP = 90% of $\textsf{₹}$ 120
Convert 90% to a fraction: $90\% = \frac{90}{100}$
SP = $\frac{90}{100} \times \textsf{₹}\ 120$
SP = $\frac{9}{10} \times \textsf{₹}\ 120$
SP = $\textsf{₹}\ \frac{9 \times 120}{10}$
SP = $\textsf{₹}\ 9 \times 12$
SP = $\textsf{₹}\ 108$
Both methods yield the same selling price.
Answer:
The price at which the flower vase is sold is $\textsf{₹}\ 108$.
Example 13. Selling price of a toy car is ₹ 540. If the profit made by shopkeeper is 20%, what is the cost price of this toy?
Answer:
Given:
Selling Price (SP) of the toy car = $\textsf{₹}$ 540.
Profit Percentage = 20%.
To Find:
The Cost Price (CP) of the toy car.
Solution:
The profit percentage is always calculated on the Cost Price.
Let the Cost Price of the toy car be CP.
The profit amount is 20% of the Cost Price.
Profit Amount = 20% of CP
Profit Amount = $\frac{20}{100} \times \text{CP}$
Profit Amount = $\frac{1}{5} \times \text{CP}$
The Selling Price is the Cost Price plus the Profit Amount.
Selling Price (SP) = Cost Price (CP) + Profit Amount
Substitute the given SP and the expression for Profit Amount:
$\textsf{₹}\ 540 = \text{CP} + \frac{1}{5} \times \text{CP}$
Combine the terms involving CP:
$\textsf{₹}\ 540 = \left(1 + \frac{1}{5}\right) \times \text{CP}$
$\textsf{₹}\ 540 = \left(\frac{5}{5} + \frac{1}{5}\right) \times \text{CP}$
$\textsf{₹}\ 540 = \frac{6}{5} \times \text{CP}$
To find CP, multiply both sides of the equation by $\frac{5}{6}$:
$\text{CP} = \textsf{₹}\ 540 \times \frac{5}{6}$
Simplify the calculation:
$\text{CP} = \textsf{₹}\ \cancel{540}^{90} \times \frac{5}{\cancel{6}_{1}}$
$\text{CP} = \textsf{₹}\ 90 \times 5$
$\text{CP} = \textsf{₹}\ 450$
Alternate Solution:
When a profit of 20% is made, the Selling Price is 100% of the Cost Price plus the 20% profit.
Selling Price (as a percentage of CP) = 100% of CP + 20% of CP
Selling Price = (100% + 20%) of CP
Selling Price = 120% of CP
We are given that the Selling Price is $\textsf{₹}$ 540.
So, $\textsf{₹}\ 540 = 120\% \text{ of CP}$
Convert 120% to a fraction:
$120\% = \frac{120}{100}$
The equation becomes:
$\textsf{₹}\ 540 = \frac{120}{100} \times \text{CP}$
Simplify the fraction:
$\frac{120}{100} = \frac{12}{10} = \frac{6}{5}$
$\textsf{₹}\ 540 = \frac{6}{5} \times \text{CP}$
To find CP, multiply both sides by $\frac{5}{6}$:
$\text{CP} = \textsf{₹}\ 540 \times \frac{5}{6}$
$\text{CP} = \textsf{₹}\ \cancel{540}^{90} \times \frac{5}{\cancel{6}_{1}}$
$\text{CP} = \textsf{₹}\ 90 \times 5$
$\text{CP} = \textsf{₹}\ 450$
Both methods give the same Cost Price.
Answer:
The cost price of the toy car is $\textsf{₹}\ 450$.
Example 14. Anita takes a loan of ₹ 5,000 at 15% per year as rate of interest. Find the interest she has to pay at the end of one year.
Answer:
Given:
Principal amount (P) = $\textsf{₹}$ 5,000.
Rate of interest (R) = 15% per year.
Time period (T) = 1 year.
To Find:
The interest Anita has to pay at the end of one year (Simple Interest).
Solution:
We need to calculate the Simple Interest (SI).
The formula for Simple Interest is:
$SI = \frac{P \times R \times T}{100}$
... (i)
Substitute the given values of P, R, and T into the formula:
$SI = \frac{\textsf{₹}\ 5000 \times 15 \times 1}{100}$
Perform the multiplication and division:
$SI = \frac{5000 \times 15}{100}$
$SI = \frac{\cancel{5000}^{50} \times 15}{\cancel{100}}$
$SI = 50 \times 15$
Calculate the product:
$50 \times 15 = 750$
So, the Simple Interest is $\textsf{₹}$ 750.
Answer:
The interest Anita has to pay at the end of one year is $\textsf{₹}\ 750$.
Example 15. If Manohar pays an interest of ₹ 750 for 2 years on a sum of ₹ 4,500, find the rate of interest.
Answer:
Given:
Principal amount (P) = $\textsf{₹}$ 4,500.
Simple Interest (SI) = $\textsf{₹}$ 750.
Time period (T) = 2 years.
To Find:
The rate of interest (R) per year.
Solution:
We are given the Simple Interest (SI), Principal (P), and Time (T). We need to find the Rate of Interest (R).
We use the formula for calculating Simple Interest:
$SI = \frac{P \times R \times T}{100}$
To find the rate of interest (R), we can rearrange the formula:
$R = \frac{SI \times 100}{P \times T}$
Substitute the given values into the rearranged formula:
$R = \frac{\textsf{₹}\ 750 \times 100}{\textsf{₹}\ 4500 \times 2 \text{ years}}$
Perform the calculation:
$R = \frac{750 \times 100}{4500 \times 2}$
$R = \frac{75000}{9000}$
Cancel the common zeros:
$R = \frac{75}{9}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor, which is 3:
$R = \frac{\cancel{75}^{25}}{\cancel{9}_{3}}$
$R = \frac{25}{3}$
The rate of interest is usually expressed as a percentage per year. So, R is in percent.
$R = \frac{25}{3}\%$ per year
We can express $\frac{25}{3}$ as a mixed number or a decimal.
As a mixed number: $\frac{25}{3} = 8 \frac{1}{3}$
$R = 8 \frac{1}{3}\%$ per year
As a decimal: $\frac{25}{3} \approx 8.333...$
$R \approx 8.33\%$ per year
Answer:
The rate of interest is $8 \frac{1}{3}\%$ per year (or approximately 8.33% per year).
Exercise 7.2
Question 1. Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.
(b) A refrigerater bought for ₹ 12,000 and sold at ₹ 13,500.
(c) A cupboard bought for ₹ 2,500 and sold at ₹ 3,000.
(d) A skirt bought for ₹ 250 and sold at ₹ 150.
Answer:
To determine the profit or loss, we compare the Selling Price (SP) and the Cost Price (CP).
- If SP > CP, there is a Profit. Profit = SP - CP.
- If SP < CP, there is a Loss. Loss = CP - SP.
- If SP = CP, there is neither profit nor loss.
The Profit or Loss percentage is calculated on the Cost Price (CP):
Profit % = $\frac{\text{Profit Amount}}{\text{CP}} \times 100\%$
Loss % = $\frac{\text{Loss Amount}}{\text{CP}} \times 100\%$
(a) Gardening shears bought for $\textsf{₹}$ 250 and sold for $\textsf{₹}$ 325.
Cost Price (CP) = $\textsf{₹}$ 250
Selling Price (SP) = $\textsf{₹}$ 325
Since SP ($\textsf{₹}$ 325) > CP ($\textsf{₹}$ 250), there is a Profit.
Profit Amount = SP - CP = $\textsf{₹}\ 325 - \textsf{₹}\ 250 = \textsf{₹}\ 75$
Profit Percentage = $\frac{\text{Profit Amount}}{\text{CP}} \times 100\%$
Profit % = $\frac{\textsf{₹}\ 75}{\textsf{₹}\ 250} \times 100\%$
Profit % = $\frac{75}{250} \times 100\% = \frac{\cancel{75}^{3}}{\cancel{250}_{10}} \times 100\% = \frac{3}{10} \times 100\% = \frac{300}{10}\% = 30\%$
(b) A refrigerator bought for $\textsf{₹}$ 12,000 and sold at $\textsf{₹}$ 13,500.
Cost Price (CP) = $\textsf{₹}$ 12,000
Selling Price (SP) = $\textsf{₹}$ 13,500
Since SP ($\textsf{₹}$ 13,500) > CP ($\textsf{₹}$ 12,000), there is a Profit.
Profit Amount = SP - CP = $\textsf{₹}\ 13,500 - \textsf{₹}\ 12,000 = \textsf{₹}\ 1,500$
Profit Percentage = $\frac{\text{Profit Amount}}{\text{CP}} \times 100\%$
Profit % = $\frac{\textsf{₹}\ 1500}{\textsf{₹}\ 12000} \times 100\%$
Profit % = $\frac{1500}{12000} \times 100\% = \frac{15}{120} \times 100\% = \frac{\cancel{15}^{1}}{\cancel{120}_{8}} \times 100\% = \frac{1}{8} \times 100\% = \frac{100}{8}\% = 12.5\%$
(c) A cupboard bought for $\textsf{₹}$ 2,500 and sold at $\textsf{₹}$ 3,000.
Cost Price (CP) = $\textsf{₹}$ 2,500
Selling Price (SP) = $\textsf{₹}$ 3,000
Since SP ($\textsf{₹}$ 3,000) > CP ($\textsf{₹}$ 2,500), there is a Profit.
Profit Amount = SP - CP = $\textsf{₹}\ 3,000 - \textsf{₹}\ 2,500 = \textsf{₹}\ 500$
Profit Percentage = $\frac{\text{Profit Amount}}{\text{CP}} \times 100\%$
Profit % = $\frac{\textsf{₹}\ 500}{\textsf{₹}\ 2500} \times 100\%$
Profit % = $\frac{500}{2500} \times 100\% = \frac{\cancel{500}^{1}}{\cancel{2500}_{5}} \times 100\% = \frac{1}{5} \times 100\% = \frac{100}{5}\% = 20\%$
(d) A skirt bought for $\textsf{₹}$ 250 and sold at $\textsf{₹}$ 150.
Cost Price (CP) = $\textsf{₹}$ 250
Selling Price (SP) = $\textsf{₹}$ 150
Since SP ($\textsf{₹}$ 150) < CP ($\textsf{₹}$ 250), there is a Loss.
Loss Amount = CP - SP = $\textsf{₹}\ 250 - \textsf{₹}\ 150 = \textsf{₹}\ 100$
Loss Percentage = $\frac{\text{Loss Amount}}{\text{CP}} \times 100\%$
Loss % = $\frac{\textsf{₹}\ 100}{\textsf{₹}\ 250} \times 100\%$
Loss % = $\frac{100}{250} \times 100\% = \frac{\cancel{100}^{2}}{\cancel{250}_{5}} \times 100\% = \frac{2}{5} \times 100\% = \frac{200}{5}\% = 40\%$
Question 2. Convert each part of the ratio to percentage:
(a) 3 : 1
(b) 2 : 3 : 5
(c) 1 : 4
(d) 1 : 2 : 5
Answer:
To convert each part of a ratio to a percentage, we first find the total number of parts by summing the numbers in the ratio. Then, for each part, we divide it by the total number of parts to get a fraction, and finally, we multiply the fraction by 100%.
(a) 3 : 1
The given ratio is 3 : 1.
Total number of parts = $3 + 1 = 4$ parts.
Percentage of the first part (3) = $\frac{3}{\text{Total parts}} \times 100\% = \frac{3}{4} \times 100\%$
= $\frac{300}{4}\% = 75\%$
Percentage of the second part (1) = $\frac{1}{\text{Total parts}} \times 100\% = \frac{1}{4} \times 100\%$
= $\frac{100}{4}\% = 25\%$
The percentages are 75% and 25%.
(b) 2 : 3 : 5
The given ratio is 2 : 3 : 5.
Total number of parts = $2 + 3 + 5 = 10$ parts.
Percentage of the first part (2) = $\frac{2}{\text{Total parts}} \times 100\% = \frac{2}{10} \times 100\%$
= $\frac{200}{10}\% = 20\%$
Percentage of the second part (3) = $\frac{3}{\text{Total parts}} \times 100\% = \frac{3}{10} \times 100\%$
= $\frac{300}{10}\% = 30\%$
Percentage of the third part (5) = $\frac{5}{\text{Total parts}} \times 100\% = \frac{5}{10} \times 100\%$
= $\frac{500}{10}\% = 50\%$
The percentages are 20%, 30%, and 50%.
(c) 1 : 4
The given ratio is 1 : 4.
Total number of parts = $1 + 4 = 5$ parts.
Percentage of the first part (1) = $\frac{1}{\text{Total parts}} \times 100\% = \frac{1}{5} \times 100\%$
= $\frac{100}{5}\% = 20\%$
Percentage of the second part (4) = $\frac{4}{\text{Total parts}} \times 100\% = \frac{4}{5} \times 100\%$
= $\frac{400}{5}\% = 80\%$
The percentages are 20% and 80%.
(d) 1 : 2 : 5
The given ratio is 1 : 2 : 5.
Total number of parts = $1 + 2 + 5 = 8$ parts.
Percentage of the first part (1) = $\frac{1}{\text{Total parts}} \times 100\% = \frac{1}{8} \times 100\%$
= $\frac{100}{8}\% = \frac{25}{2}\% = 12.5\%$
Percentage of the second part (2) = $\frac{2}{\text{Total parts}} \times 100\% = \frac{2}{8} \times 100\% = \frac{1}{4} \times 100\%$
= $\frac{100}{4}\% = 25\%$
Percentage of the third part (5) = $\frac{5}{\text{Total parts}} \times 100\% = \frac{5}{8} \times 100\%$
= $\frac{500}{8}\% = \frac{125}{2}\% = 62.5\%$
The percentages are 12.5%, 25%, and 62.5%.
Question 3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.
Answer:
Given:
Original population of the city = 25,000.
New population of the city = 24,500.
To Find:
The percentage decrease in the population.
Solution:
First, calculate the actual decrease in the population.
Decrease in population = Original population - New population
Decrease in population = $25,000 - 24,500 = 500$
The decrease in population is 500.
To find the percentage decrease, we compare the decrease in population to the original population and multiply by 100%.
Percentage Decrease = $\frac{\text{Decrease in population}}{\text{Original population}} \times 100\%$
Substitute the values:
Percentage Decrease = $\frac{500}{25000} \times 100\%$
Simplify the fraction:
$\frac{500}{25000} = \frac{50}{2500} = \frac{5}{250} = \frac{1}{50}$
Substitute the simplified fraction back into the percentage calculation:
Percentage Decrease = $\frac{1}{50} \times 100\%$
Percentage Decrease = $\frac{100}{50}\%$
Percentage Decrease = $2\%$
Answer:
The percentage decrease in the population is 2%.
Question 4. Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the Percentage of price increase?
Answer:
Given:
Original price of the car = $\textsf{₹}\ 3,50,000$.
New price of the car next year = $\textsf{₹}\ 3,70,000$.
To Find:
The percentage of price increase.
Solution:
First, calculate the actual increase in the price of the car.
Amount of price increase = New price - Original price
Amount of price increase = $\textsf{₹}\ 3,70,000 - \textsf{₹}\ 3,50,000$
Amount of price increase = $\textsf{₹}\ 20,000$
The increase in price is $\textsf{₹}\ 20,000$.
To find the percentage of price increase, we compare the amount of increase to the original price and multiply by 100%.
Percentage Increase = $\frac{\text{Amount of price increase}}{\text{Original price}} \times 100\%$
Substitute the values:
Percentage Increase = $\frac{\textsf{₹}\ 20,000}{\textsf{₹}\ 3,50,000} \times 100\%$
Percentage Increase = $\frac{20000}{350000} \times 100\%$
Simplify the fraction by canceling common zeros:
$\frac{20000}{350000} = \frac{20}{350} = \frac{2}{35}$
Substitute the simplified fraction back into the percentage calculation:
Percentage Increase = $\frac{2}{35} \times 100\%$
Percentage Increase = $\frac{2 \times 100}{35}\%$
Percentage Increase = $\frac{200}{35}\%$
Simplify the fraction by dividing the numerator and denominator by 5:
Percentage Increase = $\frac{\cancel{200}^{40}}{\cancel{35}_{7}}\%$
Percentage Increase = $\frac{40}{7}\%$
This can be expressed as a mixed number or a decimal.
As a mixed number:
$\frac{40}{7} = 5 \frac{5}{7}$
Percentage Increase = $5 \frac{5}{7}\%$
As a decimal (approximate):
$\frac{40}{7} \approx 5.714...$
Percentage Increase $\approx$ $5.71\%$
Answer:
The percentage of price increase was $5 \frac{5}{7}\%$ (or approximately 5.71%).
Question 5. I buy a T.V. for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?
Answer:
Given:
Cost Price (CP) of the T.V. = $\textsf{₹}\ 10,000$.
Profit Percentage = 20%.
To Find:
The Selling Price (SP) of the T.V.
Solution:
The profit is calculated as a percentage of the Cost Price.
First, calculate the amount of profit in Rupees.
Profit Amount = Profit Percentage of Cost Price
Profit Amount = 20% of $\textsf{₹}\ 10,000$
Convert 20% to a fraction: $20\% = \frac{20}{100}$
Profit Amount = $\frac{20}{100} \times \textsf{₹}\ 10,000$
Profit Amount = $\frac{1}{5} \times \textsf{₹}\ 10,000$
Profit Amount = $\textsf{₹}\ \frac{10000}{5}$
Profit Amount = $\textsf{₹}\ 2000$
The amount of profit is $\textsf{₹}\ 2000$.
The Selling Price is calculated by adding the Profit Amount to the Cost Price.
Selling Price (SP) = Cost Price (CP) + Profit Amount
SP = $\textsf{₹}\ 10,000 + \textsf{₹}\ 2000$
SP = $\textsf{₹}\ 12,000$
Alternate Solution:
When a profit of 20% is made, the Selling Price is (100% + 20%) of the Cost Price.
Selling Price Percentage = 100% + Profit Percentage
Selling Price Percentage = 100% + 20% = 120%
So, the Selling Price is 120% of the Cost Price.
Selling Price (SP) = 120% of CP
SP = 120% of $\textsf{₹}\ 10,000$
Convert 120% to a fraction:
$120\% = \frac{120}{100}$
SP = $\frac{120}{100} \times \textsf{₹}\ 10,000$
SP = $\frac{12}{10} \times \textsf{₹}\ 10,000$
SP = $\textsf{₹}\ \frac{12 \times 10000}{10}$
SP = $\textsf{₹}\ 12 \times 1000$
SP = $\textsf{₹}\ 12,000$
Both methods yield the same selling price.
Answer:
I get $\textsf{₹}\ 12,000$ for the T.V.
Question 6. Juhi sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Answer:
Given:
Selling Price (SP) of the washing machine = $\textsf{₹}\ 13,500$.
Loss Percentage = 20%.
To Find:
The price at which Juhi bought the washing machine (Cost Price, CP).
Solution:
The loss is calculated as a percentage of the Cost Price.
Let the Cost Price of the washing machine be CP.
The loss amount is 20% of the Cost Price.
Loss Amount = 20% of CP
Loss Amount = $\frac{20}{100} \times \text{CP}$
Loss Amount = $\frac{1}{5} \times \text{CP}$
The Selling Price is the Cost Price minus the Loss Amount.
Selling Price (SP) = Cost Price (CP) - Loss Amount
Substitute the given SP and the expression for Loss Amount:
$\textsf{₹}\ 13,500 = \text{CP} - \frac{1}{5} \times \text{CP}$
Combine the terms involving CP:
$\textsf{₹}\ 13,500 = \left(1 - \frac{1}{5}\right) \times \text{CP}$
$\textsf{₹}\ 13,500 = \left(\frac{5}{5} - \frac{1}{5}\right) \times \text{CP}$
$\textsf{₹}\ 13,500 = \frac{4}{5} \times \text{CP}$
To find CP, multiply both sides of the equation by $\frac{5}{4}$:
$\text{CP} = \textsf{₹}\ 13,500 \times \frac{5}{4}$
Perform the multiplication and division:
$\text{CP} = \textsf{₹}\ \frac{13500 \times 5}{4}$
$\text{CP} = \textsf{₹}\ \frac{67500}{4}$
$\text{CP} = \textsf{₹}\ 16875$
Alternate Solution:
When a loss of 20% is incurred, the Selling Price is (100% - 20%) of the Cost Price.
Selling Price Percentage = 100% - Loss Percentage
Selling Price Percentage = 100% - 20% = 80%
So, the Selling Price is 80% of the Cost Price.
Selling Price (SP) = 80% of CP
We are given that the Selling Price is $\textsf{₹}$ 13,500.
So, $\textsf{₹}\ 13,500 = 80\% \text{ of CP}$
Convert 80% to a fraction:
$80\% = \frac{80}{100} = \frac{4}{5}$
The equation becomes:
$\textsf{₹}\ 13,500 = \frac{4}{5} \times \text{CP}$
To find CP, multiply both sides by $\frac{5}{4}$:
$\text{CP} = \textsf{₹}\ 13,500 \times \frac{5}{4}$
$\text{CP} = \textsf{₹}\ \frac{13500 \times 5}{4}$
$\text{CP} = \textsf{₹}\ \frac{67500}{4}$
$\text{CP} = \textsf{₹}\ 16875$
Both methods yield the same Cost Price.
Answer:
The price at which she bought the washing machine was $\textsf{₹}\ 16,875$.
Question 7.
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find the percentage of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
Answer:
(i) Find the percentage of carbon in chalk.
Given:
The ratio of calcium, carbon, and oxygen in chalk is 10 : 3 : 12.
To Find:
The percentage of carbon in chalk.
Solution:
First, find the total number of parts in the ratio.
Total parts = Parts of Calcium + Parts of Carbon + Parts of Oxygen
Total parts = $10 + 3 + 12 = 25$ parts.
Now, find the fraction of carbon in the chalk.
Fraction of carbon = $\frac{\text{Parts of Carbon}}{\text{Total parts}}$
Fraction of carbon = $\frac{3}{25}$
To convert this fraction to a percentage, multiply the fraction by 100%.
Percentage of carbon = Fraction of carbon $\times$ 100%
Percentage of carbon = $\frac{3}{25} \times 100\%$
Percentage of carbon = $\frac{3 \times 100}{25}\%$
Percentage of carbon = $\frac{300}{25}\%$
Perform the division:
Percentage of carbon = $12\%$
Answer for (i): The percentage of carbon in chalk is 12%.
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
Given:
Weight of carbon in the chalk stick = 3g.
Percentage of carbon in chalk = 12% (from part i).
To Find:
The total weight of the chalk stick.
Solution:
Let the total weight of the chalk stick be W grams.
We know that the weight of carbon (3g) is 12% of the total weight of the chalk stick (W).
So, we can write the equation:
12% of W = 3g
Convert 12% to a fraction:
$12\% = \frac{12}{100}$
The equation becomes:
$\frac{12}{100} \times \text{W} = 3$
To solve for W, multiply both sides of the equation by $\frac{100}{12}$:
$\text{W} = 3 \times \frac{100}{12}$
Simplify the calculation:
$\text{W} = \cancel{3}^{1} \times \frac{100}{\cancel{12}_{4}}$
$\text{W} = \frac{100}{4}$
$\text{W} = 25$
The unit of weight is grams.
W = 25 g
Answer for (ii): The weight of the chalk stick is 25 g.
Question 8. Amina buys a book for ₹ 275 and sells it at a loss of 15%. How much does she sell it for?
Answer:
Given:
Cost Price (CP) of the book = $\textsf{₹}\ 275$.
Loss Percentage = 15%.
To Find:
The Selling Price (SP) of the book.
Solution:
The loss is calculated as a percentage of the Cost Price.
First, calculate the amount of loss in Rupees.
Loss Amount = Loss Percentage of Cost Price
Loss Amount = 15% of $\textsf{₹}\ 275$
Convert 15% to a fraction: $15\% = \frac{15}{100}$
Loss Amount = $\frac{15}{100} \times \textsf{₹}\ 275$
Simplify the fraction and perform the multiplication:
Loss Amount = $\frac{\cancel{15}^{3}}{\cancel{100}_{20}} \times \textsf{₹}\ 275$
Loss Amount = $\frac{3}{20} \times \textsf{₹}\ 275$
Loss Amount = $\textsf{₹}\ \frac{3 \times 275}{20}$
Loss Amount = $\textsf{₹}\ \frac{825}{20}$
Loss Amount = $\textsf{₹}\ 41.25$
The amount of loss is $\textsf{₹}\ 41.25$.
The Selling Price is calculated by subtracting the Loss Amount from the Cost Price.
Selling Price (SP) = Cost Price (CP) - Loss Amount
SP = $\textsf{₹}\ 275 - \textsf{₹}\ 41.25$
SP = $\textsf{₹}\ 233.75$
Alternate Solution:
Selling at a loss of 15% means the Selling Price is (100% - 15%) of the Cost Price.
Selling Price Percentage = 100% - Loss Percentage
Selling Price Percentage = 100% - 15% = 85%
So, the Selling Price is 85% of the Cost Price.
Selling Price (SP) = 85% of CP
SP = 85% of $\textsf{₹}\ 275$
Convert 85% to a fraction:
$85\% = \frac{85}{100}$
SP = $\frac{85}{100} \times \textsf{₹}\ 275$
Simplify the fraction and perform the multiplication:
SP = $\frac{\cancel{85}^{17}}{\cancel{100}_{20}} \times \textsf{₹}\ 275$
SP = $\frac{17}{20} \times \textsf{₹}\ 275$
SP = $\textsf{₹}\ \frac{17 \times 275}{20}$
SP = $\textsf{₹}\ \frac{4675}{20}$
SP = $\textsf{₹}\ 233.75$
Both methods yield the same selling price.
Answer:
Amina sells the book for $\textsf{₹}\ 233.75$.
Question 9. Find the amount to be paid at the end of 3 years in each case:
(a) Principal = ₹ 1,200 at 12% p.a.
(b) Principal = ₹ 7,500 at 5% p.a.
Answer:
To find the amount to be paid at the end of 3 years, we need to calculate the Simple Interest (SI) for the given Principal (P) at the given Rate (R) for the given Time (T), and then add it to the Principal.
The formula for Simple Interest is:
$\text{SI} = \frac{P \times R \times T}{100}$
The Amount (A) to be paid is:
$\text{A} = \text{P} + \text{SI}$
(a) Principal = ₹ 1,200 at 12% p.a.
Given:
Principal (P) = $\textsf{₹}\ 1,200$
Rate of Interest (R) = 12% per annum
Time period (T) = 3 years
To Find:
Amount to be paid at the end of 3 years.
Solution:
Calculate Simple Interest (SI):
$\text{SI} = \frac{1200 \times 12 \times 3}{100}$
$\text{SI} = \frac{1200 \times 36}{100}$
$\text{SI} = 12 \times 36$
$\text{SI} = 432$
The Simple Interest is $\textsf{₹}\ 432$.
Now, calculate the Total Amount (A):
$\text{A} = \text{P} + \text{SI}$
$\text{A} = \textsf{₹}\ 1200 + \textsf{₹}\ 432$
$\text{A} = \textsf{₹}\ 1632$
Answer for (a): The amount to be paid at the end of 3 years is $\textsf{₹}\ 1632$.
(b) Principal = ₹ 7,500 at 5% p.a.
Given:
Principal (P) = $\textsf{₹}\ 7,500$
Rate of Interest (R) = 5% per annum
Time period (T) = 3 years
To Find:
Amount to be paid at the end of 3 years.
Solution:
Calculate Simple Interest (SI):
$\text{SI} = \frac{7500 \times 5 \times 3}{100}$
$\text{SI} = \frac{7500 \times 15}{100}$
$\text{SI} = 75 \times 15$
$\text{SI} = 1125$
The Simple Interest is $\textsf{₹}\ 1125$.
Now, calculate the Total Amount (A):
$\text{A} = \text{P} + \text{SI}$
$\text{A} = \textsf{₹}\ 7500 + \textsf{₹}\ 1125$
$\text{A} = \textsf{₹}\ 8625$
Answer for (b): The amount to be paid at the end of 3 years is $\textsf{₹}\ 8625$.
Question 10. What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?
Answer:
Given:
Principal amount (P) = $\textsf{₹}\ 56,000$.
Simple Interest (SI) = $\textsf{₹}\ 280$.
Time period (T) = 2 years.
To Find:
The rate of interest (R) per year.
Solution:
We are given the Simple Interest (SI), Principal (P), and Time (T). We need to find the Rate of Interest (R).
We use the formula for calculating Simple Interest:
$\text{SI} = \frac{P \times R \times T}{100}$
To find the rate of interest (R), we rearrange the formula:
$\text{R} = \frac{\text{SI} \times 100}{P \times T}$
Substitute the given values into the formula:
$\text{R} = \frac{\textsf{₹}\ 280 \times 100}{\textsf{₹}\ 56000 \times 2 \text{ years}}$
Perform the calculation:
$\text{R} = \frac{280 \times 100}{56000 \times 2}$
$\text{R} = \frac{28000}{112000}$
Cancel the common zeros from the numerator and denominator:
$\text{R} = \frac{28}{112}$
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor, which is 28:
$\text{R} = \frac{\cancel{28}^{1}}{\cancel{112}_{4}}$
$\text{R} = \frac{1}{4}$
The rate of interest is expressed as a percentage per year. So, R is in percent.
$\text{R} = \frac{1}{4}\%$ per year
This can also be written as a decimal percentage:
$\frac{1}{4} \% = 0.25 \%$
Answer:
The rate that gives $\textsf{₹}\ 280$ as interest on a sum of $\textsf{₹}\ 56,000$ in 2 years is $\frac{1}{4}\%$ per year or 0.25% per year.
Question 11. If Meena gives an interest of ₹ 45 for one year at 9% rate p.a.. What is the sum she has borrowed?
Answer:
Given:
Simple Interest (SI) = $\textsf{₹}\ 45$.
Time period (T) = 1 year.
Rate of interest (R) = 9% per annum.
To Find:
The principal amount (P) that was borrowed.
Solution:
We are given the Simple Interest (SI), Time (T), and Rate (R). We need to find the Principal (P).
We use the formula for calculating Simple Interest:
$\text{SI} = \frac{P \times R \times T}{100}$
To find the principal amount (P), we can rearrange the formula:
$P \times R \times T = \text{SI} \times 100$
$\text{P} = \frac{\text{SI} \times 100}{R \times T}$
Substitute the given values into the formula:
$\text{P} = \frac{\textsf{₹}\ 45 \times 100}{9 \text{ \% p.a.} \times 1 \text{ year}}$
Perform the calculation:
$\text{P} = \frac{45 \times 100}{9 \times 1}$
$\text{P} = \frac{4500}{9}$
Perform the division:
$\text{P} = 500$
The principal amount is in Rupees.
P = $\textsf{₹}\ 500$
Answer:
The sum Meena has borrowed is $\textsf{₹}\ 500$.

